J GRADIENT | Research & Development

Company logo. 'J Gradient' with a blue triangle, pointing down, in front of the letter 'J', a right-pointing arrow above the word 'Gradient', and the text 'Research & Development' below, in a smaller print.
Photo of Jan Prokaj, Ph.D.

Jan Prokaj, Ph.D.

Founder

Multi-rate numerical techniques for diffusion problems in one spatial dimension

Summary

Diffusion problems arise in many branches of science and engineering. The one-dimensional diffusion equation is solved using a multi-rate numerical algorithm. The algorithm divides the system into different parts or blocks, allowing each block to take different time steps.

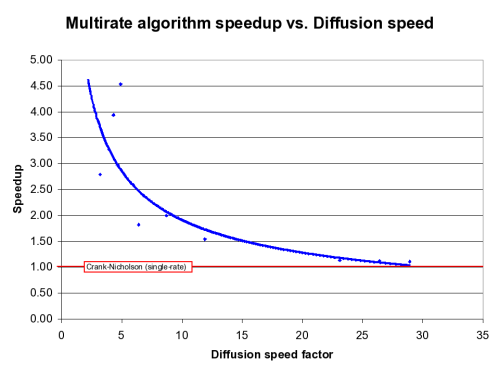
For each of the three initial profiles studied in tandem with three representative diffusion coefficient dependences, there is a very significant speedup over a Crank-Nicholson time-stepping scheme without blocking. The greatest speedup (by a factor of 5 in certain cases) is obtained for a linear diffusion with relatively small diffusion coefficient. Diffusion speed and block size are found to be major factors affecting the performance of this algorithm. Implementation of this algorithm for a two-dimensional diffusion is possible, and even greater speedups are expected in that case, since the second dimension allows for the inactive block(s) to occupy larger fractions of the overall domain.

Multirate timestepping

  • Divides the diffusion system in multiple blocks
  • Each block has different timestepping rate
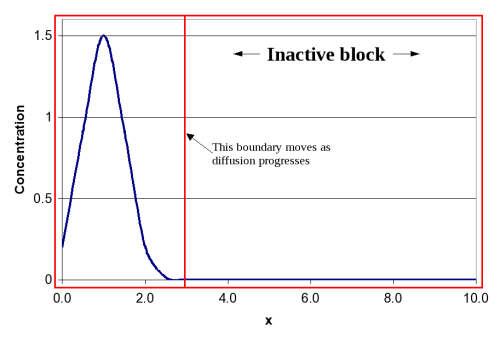
    • Active blocks updated frequently
    • Inactive blocks rarely
  • Block boundaries updated as necessary
Diffusion system
Example of a division of a diffusion system into two blocks. The inactive block is timestepped rarely, which allows for a faster solution.

Implementation

  • 2 implementations
    • Fixed blocking (updates inactive block at a fixed interval)
    • Automatic blocking (updates inactive block whenever necessary)
  • Crank-Nicholson numerical method used as a base
  • Equation discretized using box method
  • Diffusion model: D(C) = αC + β
  • Neumann boundary conditions
  • 2 blocks
  • Tridiagonal matrix solver
  • Written in C language
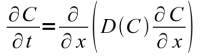
Diffusion equation
One-dimensional diffusion equation. C is concentration, t is time, x is spatial dimension, D(C) is diffusion coefficient.

What was tested

  • 3 initial profiles:
    1. 0.75*e-0.5*(x-1)2
    2. 3.50*e-4.0*(x-1)2
    3. 1.50*e-2.0*(x-1)2
  • Timestep size: 0.025, 0.05, 0.01
  • Gridstep size: 0.025, 0.05, 0.01
  • Nonlinear diffusion (α = 1.5, β = 0.02)
  • Linear diffusion
    • α = 0, β = 0.02
    • α = 0, β = 0.2
  • 2 implementations of multirate algorithm
    • Fixed blocking
    • Automatic blocking
Graph of initial profiles
Graph of the three initial concentration profiles.

Results

Graph showing speedup vs. diffusion speed
Relative diffusion speed is one of the major constraints on the use of a multirate algorithm. As the diffusion speeds up, the inactive block is updated as often as the active block, essentially turning into a single-rate algorithm.
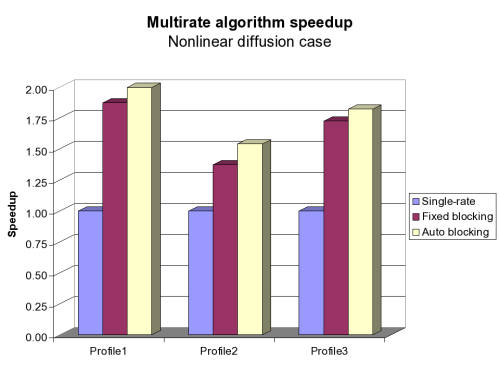
Graph showing implementation vs. speedup
In this particular case, Automatic blocking performed slightly faster than Fixed blocking. This was not true in all cases. The algorithms’ overall performance is about the same. The differences in speedup between different profiles are caused by their different diffusion speeds and sizes of the inactive blocks.
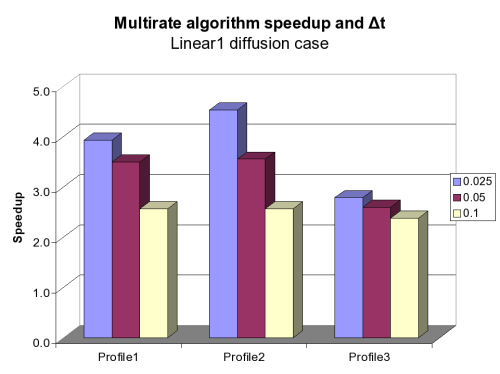
Graph showing timestep size vs. speedup
As the time step size (∆t) increases, the multirate algorithm speedup decreases. This is because concentration values change by a greater amount after a longer time interval, which in turn causes the algorithm to update the inactive block more often.
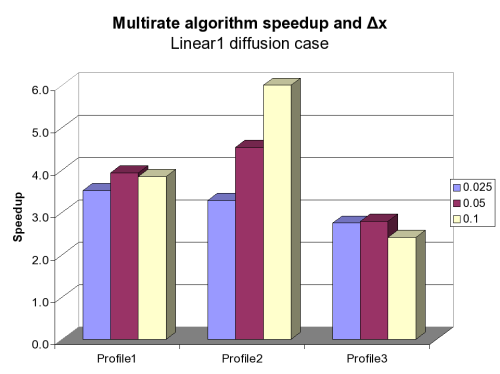
Graph showing gridstep size vs. speedup
Generally, as the grid step size (∆x) increases, the multirate algorithm speedup increases. This is because it takes more time steps to change the concentration at a gridpoint farther away, which means the algorithm is updating the inactive block less.
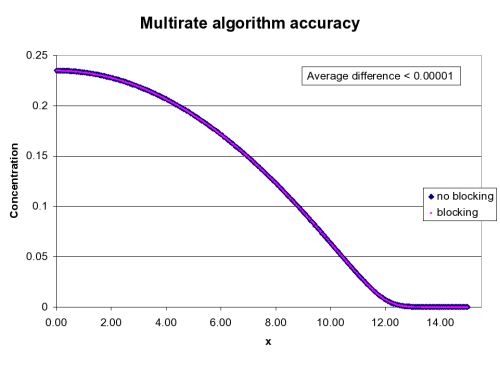
Accuracy of multirate vs. singlerate algorithm
There is almost no difference in accuracy between a multirate algorithm and a single-rate algorithm (no blocking). This largely depends on a concentration value that is set to divide the system into blocks. In this case, this value was set to 0.00001.

Conclusions

  • Multirate numerical methods produce significant speedup over single-rate methods
  • Magnitude of speedup depends on:
    • Diffusion speed
    • Size of the inactive block
    • Timestep size (smaller --> greater speedup)
    • Gridstep size (greater --> greater speedup)
  • Automatic blocking better than Fixed blocking
    • No calculation necessary to determine the frequency of updating the inactive block in Automatic blocking
    • But, no significant difference in speedup
  • Almost no loss of accuracy in the multirate algorithm
    • Depends on the concentration value used to divide the system into blocks

Acknowledgements

This project was supported by a SMART grant.

Reference

J. Prokaj , S. Roy Choudhury. Multi-rate numerical techniques for diffusion problems in one spatial dimension. Internat. J. Appl. Sci. Comput , 13(3):126-137, 2006.